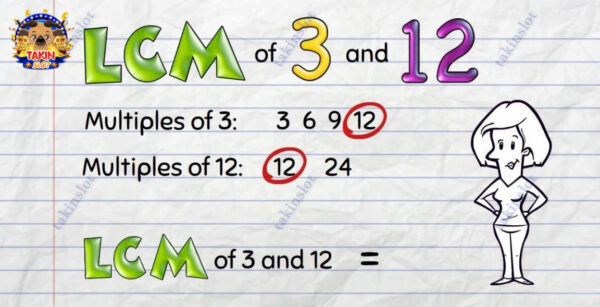LCM Full Form: In the subject of mathematics, LCM holds a significant position as it constitutes an essential lesson. Hence, it is imperative to comprehend the full form of LCM, which stands for “Least Common Multiple.” Let’s delve deeper into the concept of LCM and explore how it can be understood and applied effectively.

Introduction to LCM: LCM Full Form

LCM, or Least Common Multiple, is a fundamental concept in mathematics that is crucial for various arithmetic operations. It represents the smallest common multiple shared by two or more given numbers.

LCM Full Forms – From Different Category

LCM	Least Common Multiple
LCM	Lowest Common Multiple
LCM	Life Cycle Management
LCM	London College of Music
LCM	Laser-Capture Microdissection
LCM	Lighting Control Module
LCM	Liquid Crystal Module
LCM	Lymphocytic Choriomeningitis
LCM	Leeds College of Music
LCM	Long Course Meters
LCM	Lower of Cost or Market
LCM	Liquid Crystal Display Module
LCM	Liquid Composite Molding
LCM	Landing Craft, Mechanized
LCM	Life Cycle Model
LCM	Little Cypress-Mauriceville High School
LCM	Life Cycle Manager
LCM	Leadership and Change Management
LCM	Loss Cost Multiplier
LCM	Liquid Composite Molding
LCM	Linux Cluster Manager
LCM	Lat Computer Manager
LCM	Landesk Configuration Manager
LCM	Login Client Module
LCM	Large Core Memory
LCM	Lat Communications Manager
LCM	Life Cycle Methodology
LCM	Left Click Menu
LCM	Lost Circulation Material
LCM	Lutheran Church of the Master
LCM	Louisiana Children’s Museum
LCM	Loss Control Management
LCM	Landing Craft Medium
LCM	Letalski Center Maribor
LCM	Left Costal Margin
LCM	Sisters of the Little Company of Mary
LCM	Leadership Competency Model
LCM	London Canal Museum
LCM	Living Computer Museum
LCM	Loose Cubic Meter
LCM	Life Cycle Monitoring
LCM	Leather Case for Motorola
LCM	Line Control Module
LCM	Large-Capacity Magazine
LCM	Lawton Chiles Middle
LCM	Local Church Ministry
LCM	Large Case Management
LCM	Lead Containing Material
LCM	Live Current Media
LCM	Logistics Cost Management
LCM	Live Country Music
LCM	Loss Control Manual
LCM	Love, Courtship and Marriage
LCM	Low Cost Media
LCM	Liaison Committee Meeting
LCM	Lotsoff Capital Management
LCM	Low Cost Move
LCM	Legal & Compliance Management
LCM	LEAF Creation Method
LCM	Laser Countermeasure
LCM	Latitude Capital Management
LCM	Legal Costs Management
LCM	Line Concentrating Module
LCM	logical computing machine
LCM	Loyal Clan Member
LCM	Light Carrying Medium
LCM	Logistics Community Manager
LCM	Logic Control Module
LCM	Line Cost Model
LCM	Liquid Cooling Module
LCM	Level Converter Module
LCM	Launch Confirmation Message
LCM	Lens-CCD Module
LCM	Locally Corrected Nystrom Method
LCM	Lyreco Core Model
LCM	Linear Coded Modulation
LCM	Line Carrier Module
LCM	Lake Champlain and Moriah

Exploring LCM: LCM Full Form

To understand LCM comprehensively, one must first grasp the fundamentals of multiples and common multiples. Below, we discuss the step-by-step process of understanding and finding LCM:

Understanding Multiples:

Before diving into LCM, it is essential to understand the concept of multiples. Multiples are obtained by multiplying a given number by natural numbers (1, 2, 3, …). For example, the multiples of 3 include 3, 6, 9, 12, and so forth.

Finding Common Multiples:

Identifying common multiples is the next step in understanding LCM. Common multiples are those that are divisible by all the numbers under consideration.

Determining LCM: LCM Full Form

Once the common multiples are identified, LCM is found by selecting the smallest multiple that is divisible by each of the given numbers. It serves as the least common denominator among the numbers being analyzed.

Key Principles of Multiples:

To effectively find multiples and subsequently determine LCM, it is essential to understand some basic principles:

• Every number is a multiple of itself.
• All natural numbers are multiples of 1.
• Every multiple of a number is greater than or equal to the number itself.
• Multiples of a particular number are infinite.
• There is no greatest multiple for a given number.
• Mastery of multiplication is essential for finding multiples accurately.

Finding Multiples

To find the multiples of a given number, we simply multiply that number by successive natural numbers starting from 1, such as 1, 2, 3, 4, and so forth.

Let’s illustrate this with an example, considering the first few multiples of 4:

• 4×1=4
• 4×1=4
• 4×2=8
• 4×2=8
• 4×3=12
• 4×3=12
• 4×4=16
• 4×4=16
• 4×5=20
• 4×5=20
• 4×6=24
• 4×6=24
• 4×7=28
• 4×7=28
• 4×8=32
• 4×8=32
• 4×9=36
• 4×9=36
• 4×10=40
• 4×10=40

Thus, the multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 36, and 40. Additionally, you can continue this process to find more multiples of 4, or any other number.

This method provides a straightforward approach to finding multiples of any given number. Once you understand this process, you can proceed to learn how to find common multiples of multiple numbers.

Finding Common Multiples Using the Listing Method

Finding common multiples involves a straightforward process. A common multiple is a number that is divisible by two or more given numbers.

To find common multiples, you first need to determine the multiples of each number individually. Then, by comparing these lists, you can identify the common multiples. Let’s illustrate this with an example of finding the common multiples of 2 and 3:

• Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26…
• Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36…

By examining the lists of multiples, we can identify the common multiples of 2 and 3, which are 6, 12, 18, 24, and so on.

Using this method, you can easily find the common multiples of any two numbers.

Finding Common Multiples Using Prime Factorisation – Understanding LCM

To determine common multiples using the prime factorisation method, you must first understand prime factorisation. Once you’ve grasped prime factorisation, finding common multiples becomes straightforward.

Understanding Prime Factorisation

Prime factorisation refers to expressing a number as a product of its prime factors, where prime factors are prime numbers that multiply together to yield the original number.

There are two primary methods for finding prime factorisation:

• Factor Tree Method of Prime Factorisation
• Common Division Method of Prime Factorisation

Finding Prime Factorisation Using the Factor Tree Method

The Factor Tree Method provides a simple and effective approach to determine the prime factorisation of any number. Follow these steps to find the prime factorisation:

Begin by identifying the smallest prime factor of the given number. For example, if we have the number 24, the smallest prime factor is 2.

Once you have identified the smallest prime factor, divide the number by this prime factor. In the case of 24, divide it by 2 to get 12.

Repeat the process for the resulting quotient. Find the smallest prime factor of 12, which is also 2, and divide 12 by 2 to get 6.

Continue this process until you reach a point where the resulting quotient is a prime number. In this example, after dividing 6 by 2, we get 3, which is a prime number.

Once you have reached a prime number in the last row, you have found the prime factorisation of the original number. In this case, the prime factorisation of 24 is 2 × 2 × 2 × 3.

The Factor Tree Method is a straightforward and efficient way to find the prime factorisation of any number. Now, let’s explore another method for finding prime factorisation.

Finding Prime Factorisation Using Common Division

Prime factorisation is a straightforward process that involves only division to determine the prime factors of a given number. Follow these steps to find the prime factorisation using the common division method:

• Start by dividing the given number by its smallest prime factor.
• Then, continue dividing the resulting quotient by its smallest prime factor.
• Repeat this division process until you obtain a prime number as the quotient.
• Stop the division process when you reach a point where the quotient is a prime number.
• The prime factors obtained through this division process represent the prime factorisation of the original number.

Using this method, you can easily find the prime factorisation of any number. Now, let’s move on to understanding how to find common multiples.

How to Find Common Multiples Using Prime Factorisation

To determine the common multiples using prime factorisation, you can employ either of the prime factorisation methods available.

Begin by finding the multiples of both numbers using any prime factorisation technique. Once you have calculated the multiples of each number, compare them to identify the common multiples.

How to Find the LCM?

There are various methods to find the Least Common Multiple (LCM):

• Multiples Listing Method
• Common Division Method
• Prime Factorisation Method
• Factor Tree Method
• Division Method

Using the Listing Method to Find the LCM

To find the Least Common Multiple (LCM), follow these steps:

Determine the first few multiples of each number.

For example, consider the multiples of 2 and 3:

• Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26…
• Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36…

Identify the common multiples of 2 and 3, which are 6, 12, 18, 24.

Hence, the Least Common Multiple (LCM) is 6.

Using this method, you can efficiently find the LCM of any given numbers.

How To Find The LCM Using the Common Division Method

The Common Division Method offers several conditions to consider:

• LCM can be found for multiple numbers simultaneously using the Common Division Method.
• When using the Common Division Method to find the LCM, start dividing from 2 onwards.

While finding the LCM of three or more numbers, if two numbers are divisible while the third is not, a rule applies: “If you are finding the LCM of four numbers, and at least 50% of the numbers are divisible, proceed with those numbers; the remaining numbers remain unchanged.”

Let’s illustrate with an example: finding the LCM of 48, 72, and 108.

LCM = 2 × 2 × 3 × 3 × 2 × 2 × 1 × 3 = 432

How To Find The LCM Using the Prime Factorisation Method

Dear friends, we have discussed how to find Common Multiples using the Prime Factorisation method. Therefore, you can also find the LCM using the Prime Factorisation method. Remember, both Prime Factorisation methods can be employed to determine the LCM.

Lastly, let’s reiterate the full form of LCM: Least Common Multiples.

Final Note on LCM Full Form

Now you have acquired knowledge about the LCM full form and how to determine the LCM of any number.

If you find any issues with the post, feel free to suggest better ideas to enhance its quality. If you found the post helpful, consider sharing it with your friends.